P&K 3950
Beispiel: Kalibrierung Staubkonzentrationsmeßgerät
Product has been archived / Produkt wurde archiviert
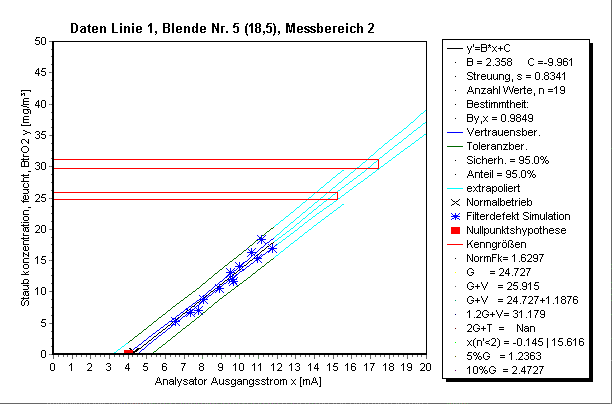
Daten Linie 1, Blende Nr. 5 (18,5), Messbereich 2
| NR | Datum | Beginn | Ende | Dauer | Analysator Ausgangsstrom | Staub konzentration, Norm, BtrO2 | Staub konzentration, feucht, BtrO2 | Staub konzentration, Norm, 11% O2 | Status | Temperatur | Feuchte | Mittl. O2-Gehalt |
|---|
| [] | [] | [] | [] | [min] | [mA] | [mg/m³] | [mg/m³] | [] | [] | [°C] | [%] | [Vol.%] |
|---|
| 1 | 17.08.99 | 13:40 | 14:12 | 32 | 8.02 | 15.4 | 8.8 | 13.9 | Filterdefekt Simulation | 105 | 21.1 | 9.9 |
| 2 | 17.08.99 | 14:17 | 14:57 | 40 | 8.88 | 18.6 | 10.6 | 16.9 | Filterdefekt Simulation | 105 | 21.1 | 10.0 |
| 3 | 17.08.99 | 15:01 | 15:31 | 30 | 6.52 | 9.1 | 5.2 | 8.3 | Filterdefekt Simulation | 105 | 21.1 | 10.1 |
| 4 | 17.08.99 | 15:58 | 16:29 | 31 | 4.35 | 0.5 | 0.3 | 0.5 | Normalbetrieb | 105 | 21.1 | 10.0 |
| 5 | 17.08.99 | 16:33 | 17:04 | 31 | 4.33 | 0.5 | 0.3 | 0.5 | Normalbetrieb | 105 | 21.1 | 10.3 |
| 6 | 18.08.99 | 08:28 | 09:01 | 33 | 4.27 | 0.5 | 0.3 | 0.5 | Normalbetrieb | 102 | 20.636 | 10.4 |
| 7 | 18.08.99 | 09:11 | 09:44 | 33 | 4.36 | 0.5 | 0.3 | 0.5 | Normalbetrieb | 103 | 20.636 | 10.6 |
| 8 | 18.08.99 | 11:02 | 11:33 | 31 | 9.64 | 20 | 11.6 | 19.2 | Filterdefekt Simulation | 102 | 20.636 | 10.6 |
| 9 | 18.08.99 | 11:43 | 12:14 | 31 | 11.74 | 29.5 | 17.0 | 28.1 | Filterdefekt Simulation | 103 | 20.636 | 10.5 |
| 10 | 18.08.99 | 12:17 | 12:48 | 31 | 10.93 | 26.4 | 15.3 | 23.8 | Filterdefekt Simulation | 102 | 20.636 | 9.9 |
| 11 | 18.08.99 | 15:51 | 16:22 | 31 | 7.77 | 12.6 | 7.1 | 12.0 | Filterdefekt Simulation | 103 | 22.845 | 10.5 |
| 12 | 18.08.99 | 16:28 | 16:57 | 29 | 7.33 | 11.9 | 6.7 | 10.7 | Filterdefekt Simulation | 103 | 22.845 | 9.9 |
| 13 | 19.08.99 | 08:41 | 09:12 | 31 | 9.97 | 24.1 | 14.0 | 21.7 | Filterdefekt Simulation | 102 | 20.24 | 9.9 |
| 14 | 19.08.99 | 09:53 | 10:24 | 31 | 9.61 | 20.7 | 12.0 | 20.7 | Filterdefekt Simulation | 102 | 20.24 | 11.0 |
| 15 | 19.08.99 | 10:32 | 11:09 | 37 | 9.48 | 22.6 | 13.1 | 21.9 | Filterdefekt Simulation | 102 | 20.24 | 10.7 |
| 16 | 19.08.99 | 11:24 | 11:59 | 35 | 11.17 | 31.9 | 18.4 | 29.3 | Filterdefekt Simulation | 104 | 20.24 | 10.1 |
| 17 | 19.08.99 | 12:37 | 13:08 | 31 | 10.6 | 28.3 | 16.3 | 27.7 | Filterdefekt Simulation | 104 | 20.24 | 10.8 |
| 18 | | | | 0 | 4 | 0 | 0.0 | 0.0 | Nullpunktshypothese | 0 | 0 | 0.0 |
| 19 | | | | 0 | 4 | 0 | 0.0 | 0.0 | Nullpunktshypothese | 0 | 0 | 0.0 |
BetrO2: bezogen auf Betriebsbedingungen, beim mittleren Wasserdampfanteil 0.213 kg/m3, beim vorhandenen Betriebs-O2-Gehalt.
Kennwerte
Funktion: y'=B*x+C
| Koeffizienten | | |
| Streuung | s | 0.8341 |
| Bestimmtheitsmaß | | 0.9849 |
| Mittelwerte | | |
| Rechenwerte | | |
Liste der Funktionswerte
| x | y' | Vertrauensbereich | Toleranzbereich | n' |
|---|
| | | y1 | y2 | y3 | y4 | |
|---|
| 4.0000 | -0.529 | -1.218 | 0.1599 | -2.984 | 1.9257 | 6.5302 |
| 4.7810 | 1.3127 | 0.7144 | 1.9110 | -1.103 | 3.7287 | 8.6580 |
| 5.5620 | 3.1543 | 2.6361 | 3.6725 | 0.7687 | 5.5399 | 11.540 |
| 6.3430 | 4.9959 | 4.5417 | 5.4502 | 2.6319 | 7.3600 | 15.016 |
| 7.1240 | 6.8376 | 6.4235 | 7.2516 | 4.4858 | 9.1893 | 18.076 |
| 7.9050 | 8.6792 | 8.2745 | 9.0838 | 6.3302 | 11.028 | 18.925 |
| 8.6860 | 10.521 | 10.093 | 10.949 | 8.1649 | 12.877 | 16.908 |
| 9.4670 | 12.362 | 11.883 | 12.842 | 9.9902 | 14.735 | 13.471 |
| 10.248 | 14.204 | 13.653 | 14.755 | 11.806 | 16.602 | 10.192 |
| 11.029 | 16.046 | 15.409 | 16.682 | 13.614 | 18.478 | 7.6465 |
| 11.810 | 17.887 | 17.157 | 18.618 | 15.414 | 20.361 | 5.8061 |
Vertrauensbereich:
Gültig für 95.0 %ige statistische Sicherheit mit Tabellenwert t(17)= 2.1106
Toleranzbereich:
Gültig für 95.0 %ige statistische Sicherheit mit Tabellenwert v(17)= 1.4004 und einem Anteil (1-gamma)=95.0 % der Gesamtheit
Funktionsvergleich ( Signifikanztest )
Koeffizienten und Streuung zu den Funktionen:
| Ansatz | Funktion | s | A | B | C |
|---|
| 1 | y'=B*x+C | 0.8341 | | 2.358 | -9.961 |
| 2 | y'=A*x²+B*x+C | 0.7848 | 0.06224 | 1.427 | -6.942 |
| 3 | y'=B*ln(x)+C | 1.406 | | 16.07 | -23.45 |
| 4 | y'=A*ln²(x)+B*ln(x)+C | 0.7667 | 12.25 | -30.22 | 18.32 |
| 5 | y'=B*exp(x)+C | 4.674 | | 1.459E-04 | 5.419 |
| 6 | y'=A*exp²(x)+B*exp(x)+C | 3.307 | -2.668E-09 | 4.309E-04 | 3.579 |
Der quadratische Ansatz kann nicht als besser angesehen werden als der lineare Ansatz.
| Prüfgröße: | 3.2008 |
| Tabellenwert F(16): | 4.4975 |
| Statistische Sicherheit: | 95% |
Es werden nur Ansatz 1. und 2. verglichen.
Kenngrößen / Grenzwerte
| | (Betriebzustand) | | (Normzustand) |
|---|
| Name | Faktor | Typ | Y-Wert | Y(Typ) | delta Y | X | Y-Wert | Y(Typ) | delta Y |
|---|
| G | 1 | -- | 24.727 | | | 14.710 | 40.297 | | |
| G+V | 1 | +V | 24.727 | 25.914 | 1.1876 | 15.214 | 40.297 | 42.233 | 1.9354 |
| 1.2G+V | 1.2 | +V | 29.672 | 31.179 | 1.5073 | 17.446 | 48.356 | 50.812 | 2.4564 |
| 2G+T | 2 | +T | 49.454 | | | | 80.595 | | |
| (n'<2) | | +T | 24.111 | 2.7504 | 26.861 | 15.616 | 39.294 | 43.776 | 4.4823 |
| 5%G | 0.05 | -- | 1.2363 | | | 4.7491 | 2.0148 | | |
| 10%G | 0.1 | -- | 2.4727 | | | 5.2728 | 4.0297 | | |
Normierungsfaktor = 1.6297


